Bij een duivenwedvlucht staan alle duiven wel samen aan de startlijn, maar ze vliegen niet naar één enkele aankomstlijn. Ieder duif vliegt naar haar hok. Het is dan ook niet de duif die het eerst geklokt wordt, die de race wint, maar wel de duif met grootste gemiddelde snelheid (uitgedrukt in m/min). En die gemiddelde snelheid is het quotiënt van de afstand en de tijd.
Maar hoe bereken je de afstand tussen 2 plaatsen op een wereldbol, die dus per definitie bolvormig is (maar ook niet perfect bolvormig)?
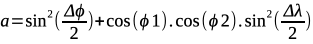
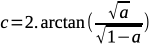
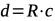
Waarbij:
- ϕ1, ϕ2: breedtegraden van de twee punten (in radialen);
- λ1, λ2: lengtegraden van de twee punten (in radialen);
- Δϕ=ϕ2−ϕ1: verschil in breedtegraad;
- Δλ=λ2−λ1: verschil in lengtegraad;
- R: de straal van de bol;
- d: de uiteindelijke afstand tussen de twee punten.
Vooraleer deze formule toe te passen om de afstand te berekenen tussen de lossingsplaats en het duivenhok moeten echter nog 2 problemen bekeken worden:
Afplatting
De aarde is niet perfect bolvormig, maar afgeplat naar de polen toe. De factor R is dus geen constante. De gemiddelde straal van de aarde is ongeveer 6371 km.
De variërende straal van de aardbol speelt enkel een rol voor vluchten met een verschil in noorderbreedte. Dat is dus het geval voor duivenwedvluchten, die in West-Europa bijna altijd van zuid naar noord gevlogen worden. Voor de zogenaamde snelheidsvluchten (tot ongeveer 200 km) kan wellicht zonder grote fout gewerkt worden met een constante R, de gemiddelde straal over het traject van de vlucht.
De vraag is of dat nog geldt voor de zware fondvluchten. De afstand tot een hok in Noord-Frankrijk is voor Barcelona ongeveer 850 km, maar voor Friesland loopt dat op tot 1350 km. Is er dan nog sprake van een eerlijke uitslag als voor de afstandsbepaling van beide hokken een constante R wordt gebruikt?
Grootcirkelafstand
De Haversine formule berekent de “grootcirkelafstand”, dat is dan wel de afstand van het kortste traject tussen twee punten, maar dat traject op een Mercator projectie is geen rechte lijn. Een vliegtuig dat de grootcirkel volgt moet daarom continu zijn koers aanpassen.
De vraag is dan of een duif de grootcirkel volgt. Het antwoord: we weten nog steeds niet hoe een duif de weg naar haar hok bepaalt. Misschien hangt ze wel vast aan haar hok met een virtuele elastiek en dan volgt ze inderdaad de grootcirkel.
De grootcirkel is enkel van belang voor vluchten met een verschil in lengtegraad, en bij een hoge noorderbreedte (dus dicht bij de polen). Dat soort wedvluchten zijn zeldzaam in de West-Europese duivenwereld1.
1In tijden van vogelpest gebeurt het dat de grens met Frankrijk gesloten is voor duivenvervoer (dat was ook het geval tijdens de coronaperiode). Toen werden er inderdaad vluchten ingericht van oost naar west.